Fractal Geometry
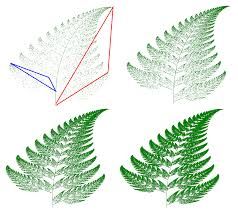
Traditional mathematics assumed that geometric shapes had smooth edges, more like the shapes we see in our constructed world. So in the 1960s when the iconoclastic Benoit Mandelbrot introduced the notion of rough-edge geometry that better reflected the shapes found in nature, he was initially dismissed as a fringe mathematician.
One reason why Mandelbrot's idea was treated with skepticism was that he represented "applied" mathematics, so that the fractal concept, which was vaguely familiar, was uninteresting to theoretical mathematicians.
The negative attitude quickly changed when Mandelbrot published a book, The Fractal Geometry of Nature (1982), which contained evidence and many illustrations of fractal patterns in nature. The patterns, once presented, seemed completely obvious and stimulated a great interest beyond the mathematical community.
Today, scientists and engineers in many disciplines recognize the value of fractal geometry. But among some theoretical mathematicians the idea may still be controversial.
